Coin Flip
When flipping a coin, people implicitly assume that 50% of the time they get heads, 50% of the time they get tails. But in principle, the coin can land on the edge. How thick must the coin be, in order for this probability to be exactly 50%?
To answer this question, I ran a simulation using the PyByllet physics simulation code. The probability of coin landing on the edge is show in blue in the following figure (the error bars are statistical due to limited number of simulated flips):
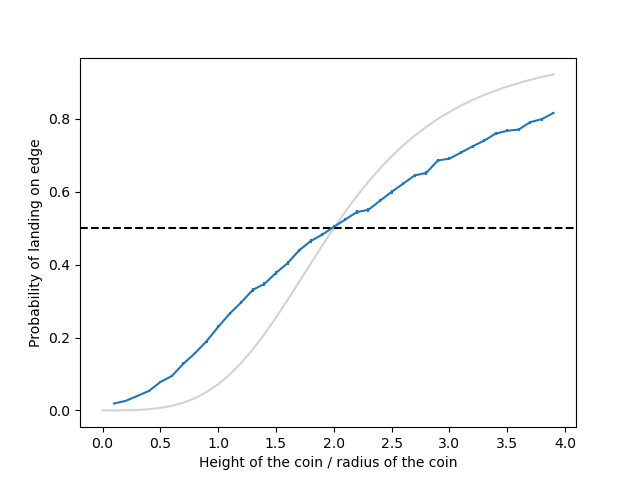
We see that to have 50% chance of edge landing, we need the thickness of the coin to be equal to twice its radius.
In the figure, the gray line shows prediction of the theoretical model from the article "Exact face-landing probabilities for bouncing objects: Edge probability in the coin toss and the three-sided die problem" . We see differences, which could be caused by any of the following:
- what I considered to be a "coin toss" (limited range of initial positions, velocities and angular momenta) does not lead to sufficient virialization in the phase space
- difference in physical parameters (restitution, friction) assumed
- issues with the simulation
I do not investigate the differences further, however it is interesting that I agree with the paper on the coin thickness that leads to the 50% edge landing probability.